■算法简介

据统计，在工业过程控制中，90％以上的控制回路具有PID结构。PID被广泛应用主要是因为它结构简单，综合了系统过去( I ) 、现在( P ) 、未来( D) 三方面信息，对动态过程无需太多的先验知识，鲁棒性强，控制效果一般令人满意， 为广大工程技术人员所熟知。

但是，PID参数的整定一直是令人困扰的问题。1942年Ziegler和Nichols得出了PID参数的工程整定法，简称Z-N整定公式；1953年 Cohen和Caan继承发展了Z-N公式，提出了考虑被控过程时滞大小的 C-C整定公式，这些方法至今仍在工业控制中普遍应用。在常规PID控制参数的整定过程中，往往技巧多于科学，整定费时费力，加之实际系统千差万别，又有滞后、非线性等因素，使得PID参数的整定较为困难，致使许多PID控制器没有能整定到较好状态。

我们根据观察和摸索，结合最新的自动控制理论和工程实践，借助当前高度发达的电子技术，实现了一种新颖的算法模型，能够实现严谨的自整定PID控制。这种控制算法的主要特点是——能够根据运行条件的变化自动调整PID控制参数，无需人为干预，从而最大限度的节省调试和后期管理工作量和难度。

算法主要流程是：

1. 自动辨识被控系统的近似模型；

2. 采取零极点对消的策略计算PID控制器的参数；

3. 根据参数实现工程PID控制器，并进行仿人智能化；

4. 当外部环境产生较大变化时，导致偏差加大，当偏差形态超过一定阈值时，再次启动上述过程，重新设计PID参数，并替代原有的参数；从而实现自整定。

第一步：在辨识被控系统的近似模型时，我们首先获取被控对象的阶跃响应；而后确定使用的近似模型种类（一般为2阶系统加入滞后环节）；最后利用特征面积计算法得到系统的近似模型参数。

第二步：在计算PID控制器的参数时，我们首先确定满足控制系统开环控制品质的开环传递函数；然后确定增益裕度和相位裕度；最后根据零极点对消原则计算出实际PID控制器的传递函数参数。（上述计算首先采用haalman法；而后根据T/L的关系动态选择PID参数整定方法（Z-N,C-C,IS）；最后综合两者获取更切合实际的PID实际控制参数）

第三步：在实现工程PID控制时，考虑死区、积分分离、工程微分设计、抗饱和等多种策略，实现高效率PID控制算法和输出。

仿人智能化是提升PID控制品质的重要因素，当前采用的智能化策略如下：

√当偏差大时，为了避免过度超调，不加入积分项，而采用倍增的比例项；

√当偏差减少后，逐步加入积分项，减小比例项；

√微分项平均分配到8个时间周期里进行，减少系统过度敏感性；

√死区动态调整，根据稳定裕度增加或者减少；（0.5度~2度之间）

√连续调节而偏差变化很小时，暂停调节，待偏差变化后，重新计算输出；

√非平衡算法，正向偏差时调节积极，负向偏差时调节保守；

√实时记录∑e、 e、∆e、∆e^2，根据4者的大小关系，调节KP,KI,KD参数的大小；

经过上述仿人智能化之后，控制效果得到明显提升，下图中是仿真计算的效果示意，从图中可以清晰看到，无论从调节时间、残差、超调、敏感性上，新的算法都有较为明显的优势。

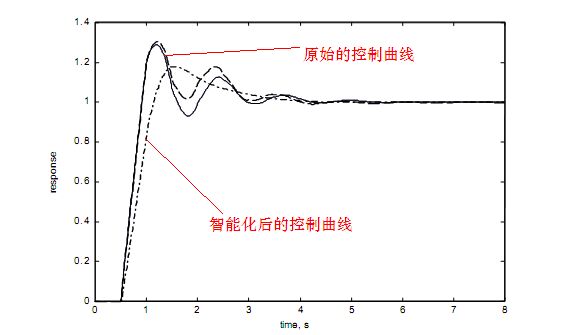
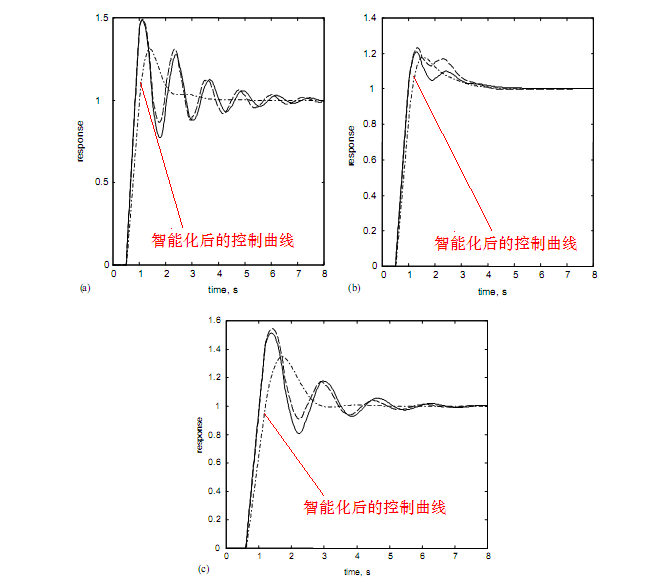
第四步：当外部环境产生较大变化时，偏差与预期的变化效果有明显的差异，当差异超过一定阈值时，启动重新计算PID参数的过程，用新的参数替代原有参数；从而实现参数自整定。

参数自整定的过程与控制算法计算的关系如下图所示：

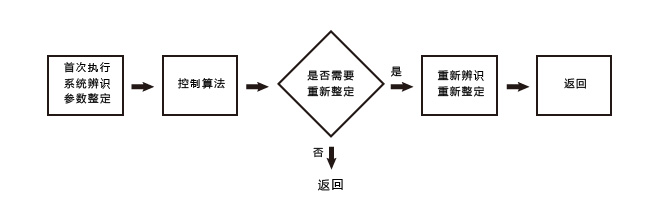
此项算法属于发明性创新，在国内外没有相类似的思路和实现过程。在供热领域更是属于革新性的使用，极大提高了温度PID控制的品质，在实践中这种控制算法的优势表现得淋漓尽致。